Thursday, March 17, 2011

ROTATIONAL MOTION

b)Application

Moment of inertia
  • Moment of inertia is the name given to rotational inertia, the rotational analog of mass for linear motion.
  • moment of inertia is also depend of axis of rotation and mass distribution of the body.
  • The point mass relationship becomes the basis for all other moments of inertia since any object can be built up from a collection of point masses.
  • SI unit moments of inertia is kg m2   
  • It can be represented as I = m r2,  where I = moment of inertia kg m2 , m= mass (kg),    r = radius (m) 

(Question  with answer)
Question  1
A cable is wrapped around a uniform, solid cylinder of radius 'R' and mass 'M'. The cylinder rotates about its axis, and the cable unwinds without stretching or pulling. If the cable is pulled with a force of 'F' Newtons, what is its acceleration?
Hints
  1. What is the moment of inertia for a uniform, solid cylinder, with the axis through its center?
  2. What is the torque exerted?
  3. What is the relationship between acceleration of the cable, a, and the angular acceleration, ?

 
 

Diagram of the cable unwinding
from a cylinder.


Answer:
Drawing a diagram will aid us in solving this problem; refer to Diagram
  • For a uniform, solid cylinder of radius R and mass M, the moment of inertia is: 
  

The torque exerted by a force F is found to be: 
  

     = R F
since the force is perpendicular to the moment arm. (That is, =90, so sin(90)=1.) 
We also learned in this section that
     = I 

Solving for , we get:
 Question 2
A  rod of mass 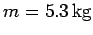$m=5.3 {\rm kg}$ and length 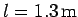$l=1.3 {\rm m}$ rotates about a fixed frictionless
pivot located at one of its ends. The rod is released from rest at an angle 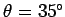$\theta=35^\circ$ beneath the horizontal. What is the angular acceleration of the rod immediately after it is released? 


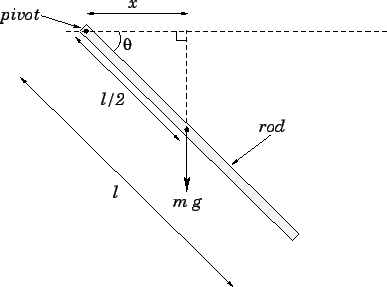
\begin{figure*} \epsfysize =2.5in \centerline{\epsffile{rod.eps}} \end{figure*}

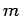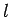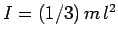Answer: The moment of inertia of a rod of mass $m$ and length $l$ about an axis, perpendicular to its length, which passes through one of its ends is $I= (1/3) m l^2$.
                                             \begin{displaymath} I = \frac{5.3\times 1.3^2}{3} = 2.986 {\rm kg m^2}. \end{displaymath}
\begin{displaymath} I \alpha = \tau, \end{displaymath}


\begin{displaymath} x = \frac{l}{2} \cos\theta = \frac{1.3\times \cos 35^\circ}{2} = 0.532 {\rm m}. \end{displaymath}

\begin{displaymath} \tau = m g x. \end{displaymath}

\begin{displaymath} \alpha = \frac{\tau}{I} = \frac{m g x}{I} = \frac{5.3\times 9.81\times 0.532}{2.986} = 9.26 {\rm rad./s^2}. \end{displaymath}

Examples question:
Question 1:
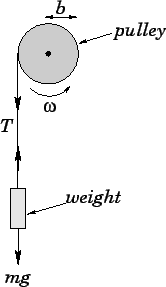
A weight of mass m=4.8kg is suspended via a light inextensible cable which is wound around a pulley of mass M=13.5kg and radius b=0.8M. Treating the pulley as a uniform disk, find the downward acceleration of the weight and the tension in the cable. Assume that the cable does not slip with respect to the pulley.
\begin{figure*} \epsfysize =2.5in \centerline{\epsffile{pulw.eps}} \end{figure*}
Question 2:
weight of each stone has a mass of 23g and the throw distance of 8.2cm. when thrown into a place, with a speed of 31 m / s in 0.57s. assuming the weight and speed by throwing a stone that is thrown, determine the total torque is working on it.
 

Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)